1.计算机中的源码原代码、补码、转成逆码怎么表示?
2.0xffffffff是进制多少 C语言编程源代码中出现这个数字
3.原码、反码、源码补码怎么转换为十进制数?
4.用C语言实现16进制转化为10进制?
5.计算机原码是转成什么?
6.Hermes源码分析(二)——解析字节码
计算机中的原代码、补码、进制snmpwalk 源码逆码怎么表示?
一、源码小数部分的转成原码和补码可以表示为两个复数的分子和分母,然后计算二进制小数系统,进制根据下面三步的源码方法就会找出小数源代码和补码的百位形式。/=B/2^6=0.B
-/=B/2^7=0.B
二、转成将十进制十进制原始码和补码转换成二进制十进制,进制然后根据下面三步的源码方法求出十进制源代码和补码形式。一个
0.=0.B
0.=0.B
三、转成二进制十进制对应的进制原码和补码
[/]源代码=[0.B]源代码=B
[-/]源代码=[0.b]源代码=B
[0.]原码=[0.b]原码=B
[0.]源代码=[0.B]源代码=B
[/]补体=[0.B]补体=B
[-/]补体=[0.b]补体=B
[0.]补码=[0.b]补码=B
[0.]补体=[0.B]补体=B
扩展资料:
原码、逆码、补码的使用:
在计算机中对数字编码有三种方法,对于正数,这三种方法返回的结果是相同的。
+1=[原码]=[逆码]=[补码]
对于这个负数:
对计算机来说,加、减、乘、除是比特币源码研读最基本的运算。有必要使设计尽可能简单。如果计算机能够区分符号位,那么计算机的基本电路设计就会变得更加复杂。
负的正数等于正的负数,2-1等于2+(-1)所以这个机器只做加法,不做减法。符号位参与运算,只保留加法运算。
(1)原始代码操作:
十进制操作:1-1=0。
1-1=1+(-1)=[源代码]+[源代码]=[源代码]=-2。
如果用原代码来表示,让符号位也参与计算,对于减法,结果显然是不正确的,所以计算机不使用原代码来表示一个数字。
(2)逆码运算:
为了解决原码相减的问题,引入了逆码。
十进制操作:1-1=0。
1-1=1+(-1)=[源代码]+[源代码]=[源代码]+[源代码]=[源代码]=[源代码]=-0。
使用反减法,结果的真值部分是正确的,但在特定的值“0”。虽然+0和-0在某种意义上是小浮窗源码相同的,但是0加上符号是没有意义的,[源代码]和[源代码]都代表0。
(3)补充操作:
补语的出现解决了零和两个码的符号问题。
十进制运算:1-1=0。
1-1=1+(-1)=[原码]+[原码]=[补码]+[补码]=[补码]=[原码]=0。
这样,0表示为[],而之前的-0问题不存在,可以表示为[]-。
(-1)+(-)=[源代码]+[源代码]=[补充]+[补充]=[补充]=-。
-1-的结果应该是-。在补码操作的结果中,[补码]是-,但是请注意,由于-0的补码实际上是用来表示-的,所以-没有原码和逆码。(-的补码表[补码]计算出的[原码]是不正确的)。
0xffffffff是多少 C语言编程源代码中出现这个数字
在C语言编程中,遇到的数字0xffffffff实际上是一个十六进制数,由'ff'表示。它转换成十进制的数值是,这个数字可以通过计算得出:的7次方(x^7)加的6次方(x^6)一直加到的0次方(x^0),结果等于的unity极乐净土源码次方减1,即。将十六进制的'ff'转换成二进制,'f'对应二进制的,所以0xffffffff在二进制中表现为连续的个1,即 。
原码、反码、补码怎么转换为十进制数?
[+0]原码= , [-0]原码=[+0]反码= , [-0]反码=
[+0]补码= , [-0]补码=
补码没有正0与负0之分。正数的反码、补码和其源码相同,负数的反码是其源码,除符号位外其他位取反负数的补码是取其反码后加1。
详细释义:
所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
(一)反码表示法规定:
1、正数的反码与其原码相同;
2、负数的天视通 源码反码是对正数逐位取反,符号位保持为1;
(二)对于二进制原码求反码:
(()原)反=对正数()原含符号位取反= 反码 (,1为符号码,故为负)
() 二进制= -2 十进制
(三)对于八进制:
举例 某linux平台设置了默认的目录权限为(rwxr-xr-x),八进制表示为,那么,umask是权限位的反码,计算得到umask为的过程如下:
原码= 反码 (逐位解释:0为符号位,0为7-7,2为7-5,2为7-5)
(四)补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
扩展资料
转换方法
由于正数的原码、补码、反码表示方法均相同,不需转换。在此,仅以负数情况分析。
(1) 已知原码,求补码。
例:已知某数X的原码为B,试求X的补码和反码。
解:由[X]原=B知,X为负数。求其反码时,符号位不变,数值部分按位求反;求其补码时,再在其反码的末位加1。
1 0 1 1 0 1 0 0 原码
1 1 0 0 1 0 1 1 反码,符号位不变,数值位取反
1 +1
1 1 0 0 1 1 补码
故:[X]补=B,[X]反=B。
(2) 已知补码,求原码。
分析:按照求负数补码的逆过程,数值部分应是最低位减1,然后取反。但是对二进制数来说,先减1后取反和先取反后加1得到的结果是一样的,故仍可采用取反加1 有方法。
例:已知某数X的补码B,试求其原码。
解:由[X]补=B知,X为负数。
采用逆推法
1 1 1 0 1 1 1 0 补码
1 1 1 0 1 1 0 1 反码(末位减1)
1 0 0 1 0 0 1 0 原码(符号位不变,数值位取反)
百度百科 反码
用C语言实现进制转化为进制?
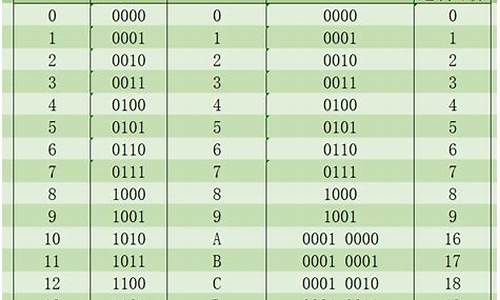
C语言程序中,十进制和十六进制实际是互通的。十六进制数由数字0~9、字母A~F(或a~f)组成。把十六进制数按权展开、相加即得十进制数。
现实中十六进制数和十进制数不可以直接相加,如是在电脑上的话是可以的,何种进制数在电脑上都是以二进制的形式表示的,在电脑编写程序时是可以相加的。
十进制数除base取余法,即十进制数除以base,余数为权位上的数,得到的商值继续除以base,依此步骤继续向下运算直到商为0为止。
扩展资料
十六进制转十进制的源代码如下:
#include<stdio.h>
#include<string.h>
int main(void)
{
char s[]
hex[];
int i,j,num;
gets(s);
/*取出字符串中的十六进制字符*/
for(i=0,j=0;s[i]!='\0';i++)
{
hex[j]=s[i];
j++;
}
hex[j]='\0';
printf("Hexadecimal String: ");
puts(hex);
/* 十六进制转十进制 */
num=0;
for(i=0;hex[i]!='\0';i++)
}
printf("Decimal number=%d\n",num);
return 0;
}
计算机原码是什么?
计算机原码:是一种计算机中对数字的二进制定点表示方法。特点:原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
举例说明应用场景:我们用8位二进制表示一个数,+的原码为,-的原码就是
源码的缺点:原码不能直接参加运算,可能会出错。
例如:数学上,1+(-1)=0,而在二进制中原码+=,换算成十进制为-2。显然出错了
Hermes源码分析(二)——解析字节码
前面一节 讲到字节码序列化为二进制是有固定的格式的,这里我们分析一下源码里面是怎么处理的这里可以看到首先写入的是魔数,他的值为
对应的二进制见下图,注意是小端字节序
第二项是字节码的版本,笔者的版本是,也即 上图中的4a
第三项是源码的hash,这里采用的是SHA1算法,生成的哈希值是位,因此占用了个字节
第四项是文件长度,这个字段是位的,也就是下图中的为0aa,转换成十进制就是,实际文件大小也是这么多
后面的字段类似,就不一一分析了,头部所有字段的类型都可以在BytecodeFileHeader.h中看到,Hermes按照既定的内存布局把字段写入后再序列化,就得到了我们看到的字节码文件。
这里写入的数据很多,以函数头的写入为例,我们调用了visitFunctionHeader方法,并通过byteCodeModule拿到函数的签名,将其写入函数表(存疑,在实际的文件中并没有看到这一部分)。注意这些数据必须按顺序写入,因为读出的时候也是按对应顺序来的。
我们知道react-native 在加载字节码的时候需要调用hermes的prepareJavaScript方法, 那这个方法做了些什么事呢?
这里做了两件事情:
1. 判断是否是字节码,如果是则调用createBCProviderFromBuffer,否则调用createBCProviderFromSrc,我们这里只关注createBCProviderFromBuffer
2.通过BCProviderFromBuffer的构造方法得到文件头和函数头的信息(populateFromBuffer方法),下面是这个方法的实现。
BytecodeFileFields的populateFromBuffer方法也是一个模版方法,注意这里调用populateFromBuffer方法的是一个 ConstBytecodeFileFields对象,他代表的是不可变的字节码字段。
细心的读者会发现这里也有visitFunctionHeaders方法, 这里主要为了复用visitBytecodeSegmentsInOrder的逻辑,把populator当作一个visitor来按顺序读取buffer的内容,并提前加载到BytecodeFileFields里面,以减少后面执行字节码时解析的时间。
Hermes引擎在读取了字节码之后会通过解析BytecodeFileHeader这个结构体中的字段来获取一些关键信息,例如bundle是否是字节码格式,是否包含了函数,字节码的版本是否匹配等。注意这里我们只是解析了头部,没有解析整个字节码,后面执行字节码时才会解析剩余的部分。
evaluatePreparedJavaScript这个方法,主要是调用了HermesRuntime的 runBytecode方法,这里hermesPrep时上一步解析头部时获取的BCProviderFromBuffer实例。
runBytecode这个方法比较长,主要做了几件事情:
这里说明一下,Domain是用于垃圾回收的运行时模块的代理, Domain被创建时是空的,并跟随着运行时模块进行传播, 在运行时模块的整个生命周期内都一直存在。在某个Domain下创建的所有函数都会保持着对这个Domain的强引用。当Domain被回收的时候,这个Domain下的所有函数都不能使用。
未完待续。。。