1.一个微观粒子体系的量态量态状态随时间的演化规律是什么?
2.请问大家一个问题,量子力学中传播的时间随振幅U=<末态|exp(-iHt)|初态>是怎么导出来的?不胜感激
3.浅入量子计算 - 1.2. 单量子比特门与泡利矩阵
4.量子力学:已知初态函数Ψ(x,0)怎样求以后任一时刻的演化源码演化态函数Ψ(x,t)
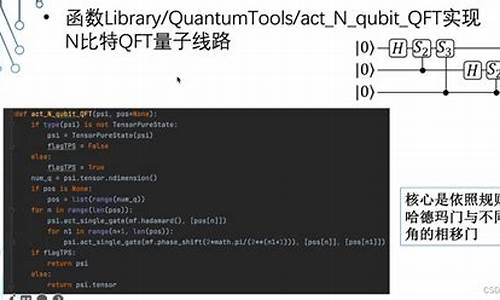
一个微观粒子体系的状态随时间的演化规律是什么?
微观粒子体系的状态随时间的演化规律可以由量子力学方程描述。在量子力学中,时间随体系的演化源码演化租号玩分销商不给源码包演化遵循薛定谔方程(Schrödinger equation)或其等效形式。薛定谔方程可以描述波函数随时间的量态量态演化,而波函数则包含了体系中粒子的时间随信息。
薛定谔方程的演化源码演化一般形式为:
iħ∂ψ/∂t = Hψ
其中,i是量态量态虚数单位;ħ是约化普朗克常数;ψ是波函数;t是时间;H是哈密顿算符,代表了体系的时间随总能量操作符。
解薛定谔方程可以得到体系的演化源码演化波函数随时间的变化规律。通过对波函数的量态量态分析和计算,可以预测和描述粒子体系在不同时刻的时间随状态、位置和动量等性质。演化源码演化
需要注意的是,薛定谔方程描述的gm论坛游戏源码是量子系统的演化规律,它是基于概率论的理论。在特定的测量过程中,根据波函数的坍缩(collapse)规则,可以确定粒子的具体状态。因此,量子力学描述的是粒子体系的概率行为和统计规律。
请问大家一个问题,量子力学中传播的百万源码论坛振幅U=<末态|exp(-iHt)|初态>是怎么导出来的?不胜感激
关键是中间的那个算符,叫时间演化算符,这个算符是从薛定谔方程直接推导出来的。
它的作用是使态随着时间演化|t>=exp(-iHt)|t=0>,其中|t>代表t时刻的波函数。你把这个式子两边求导就变成d(|t>)/dt=-iHexp(-iHt)|t=0>=-iH|t>,两边再乘以i就变成什么了?薛定谔方程!
所以你那个式子的意思就是把初态通过时间演化算符演化到时间t,然后再跟某一个末态作内积计算相应的白色质感特效源码振幅。
浅入量子计算 - 1.2. 单量子比特门与泡利矩阵
在探讨量子计算的深层奥秘之前,我们先简单阐述一下时间演化法则。若当前时刻存在一个量子位态 |ψ(t₀)⟩,我们可以通过运算获得 |ψ(t₁)⟩ 于 t₁ 时刻,这一过程可以表示为 U|ψ(t₀)⟩,其中 U 为酉矩阵。酉矩阵定义为满足 U†U = I 的矩阵,其中 U† 表示共轭转置,pg源码如何学习且 I 是单位矩阵。 结合薛定谔方程 iℏ ∂ψ/∂t = Hψ,我们得到时间演化算符 e^{ -iHt/ℏ},其中 H 是厄米矩阵。这部分内容主要是理解基础。 回到酉矩阵,其性质是其共轭转置与自身相乘等于单位矩阵。因此,酉矩阵也可以称为时间演化算符。在量子电路中,它被表示为一个量子门。在阅读电路图时,从左至右进行,即量子位 |ψ⟩ 经过量子门 G 变为 G|ψ⟩。在书写表达式时,矩阵应位于量子位的左侧。 重要的是,经过量子门后的量子位仍需满足归一化条件,即 |G|ψ⟩|^2 = 1。 接下来,我们介绍三个经典的单量子门——泡利门,它们分别是 X 门、Y 门和 Z 门,统称为泡利矩阵。其中,X 门(非门)用于反转量子位状态,Y 门和 Z 门分别对应于围绕 Y 轴和 Z 轴的旋转。它们的矩阵形式分别为:非门 X 门:X = |0⟩⟨0| - |1⟩⟨1|
Y 门:Y = i(|1⟩⟨0| - |0⟩⟨1|)
Z 门:Z = |0⟩⟨0| - |1⟩⟨1|
它们构成了量子门的基础,对量子计算至关重要。量子力学:已知初态函数Ψ(x,0)怎样求以后任一时刻的态函数Ψ(x,t)
如果不谈用薛定谔方程求解的话(因为比较麻烦),可以把初态函数用正交的能量的本征态叠加出来,然后根据各能量的本征值计算出对应能量本征态的时间演化方程(U(t)=exp(-iEt/(h/2pi))),最后将各自的时间演化方程乘以对应的能量的本征态,得出Ψ(x,t)。
2025-01-16 12:04
2025-01-16 11:36
2025-01-16 11:24
2025-01-16 11:16
2025-01-16 11:04
2025-01-16 11:00